Soptq

本文はCSDN 反向伝播アルゴリズム（プロセスと公式の導出）を深く参考にしています。

基本的な定義#

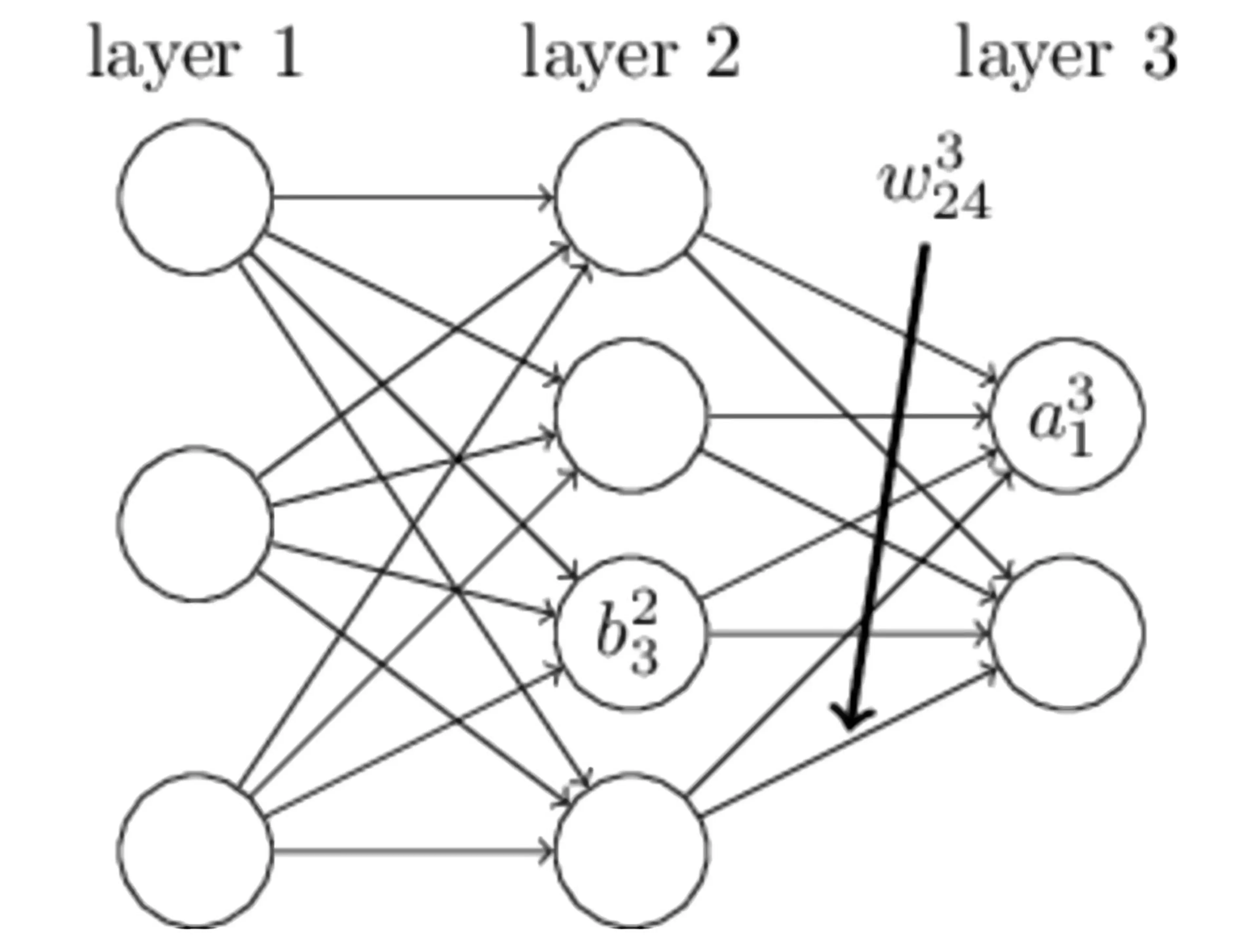
上記の図に示されている単純なニューラルネットワークでは、layer 1は入力層、layer 2は隠れ層、layer 3は出力層です。以下にいくつかの変数名の意味を説明します：

上記の定義から、次のことがわかります：

$z_{j}^{l} = \sum_{i}w_{ji}^{l}a_{i}^{l-1} + b_{j}^{l}$

$a_{j}^{l} = \sigma z_{j}^{l} = \sigma \left( \sum_{i}w_{ji}^{l}a_{i}^{l-1} + b_{j}^{l} \right)$

損失関数を二乗コスト関数（Quadratic Cost Function）とします：

$J = \frac{1}{2n} \sum_{x} \lvert \lvert y(x) - a^{L}(x) \rvert \rvert ^ {2}$

ここで、$x$は入力サンプルを表し、$y(x)$は実際の分類を表し、$a^{L}(x)$は予測された分類を表し、$L$はネットワークの最大層数を表します。入力サンプルが 1 つだけの場合、損失関数 $J$は次のようになります：

$J = \frac{1}{2} \sum_{x} \lvert \lvert y(x) - a^{L}(x) \rvert \rvert ^ {2}$

最後に、第 $l$ 層の $i$ 番目のニューロンで生成されるエラーを次のように定義します：

$\delta_{i}^{l} \equiv \frac{\partial{J}}{\partial{z_{i}^{l}}}$

公式の導出#

損失関数に対する最後の層のニューラルネットワークのエラーは次のようになります：

$\begin{aligned}\delta_{i}^{L} &= \frac{\partial{J}}{\partial{z_{i}^{L}}}\\&=\frac{\partial{J}}{\partial{a_{i}^{L}}} \cdot \frac{\partial{a_{i}^{L}}}{\partial{z_{i}^{L}}}\\&=\nabla J(a_{i}^{L}) \sigma^{'}(z_{i}^{L})\end{aligned}$

$\delta^{L} = \nabla J(a^{L}) \odot \sigma^{'}(z^{L})$

損失関数に対する $j$ 層目のネットワークのエラーは次のようになります：

$\begin{aligned}\delta_{j}^{l} &= \frac{\partial{J}}{\partial{z_{j}^{l}}} \\ &= \frac{\partial{J}}{\partial{a_{j}^{l}}} \cdot \frac{\partial{a_{j}^{l}}}{\partial{z_{j}^{l}}} \\ &= \sum_{i} \frac{\partial{J}}{\partial{z_{i}^{l+1}}} \cdot \frac{\partial{z_{i}^{l+1}}}{\partial{a_{j}^{l}}} \cdot \frac{\partial{a_{j}^{l}}}{\partial{z_{j}^{l}}} \\ &= \sum_{i} \delta_{i}^{l+1} \cdot \frac{\partial{w_{ij}^{l+1}a_{j}^{l} + b_{i}^{l+1}}}{\partial{a_{j}^{l}}} \cdot \sigma^{'}(z_{j}^{l}) \\ &=\sum_{i} \delta_{i}^{l+1} \cdot w_{ij}^{l+1} \cdot \sigma^{'}(z_{j}^{l}) \end{aligned}$

$\delta^{l} = \left( \left( w^{l+1} \right)^{T} \delta^{l+1} \right) \odot \sigma^{'}(z^{l})$

したがって、損失関数を使用して重みの勾配を計算することができます：

$\begin{aligned} \frac{\partial{J}}{\partial{w_{ji}^{l}}} &= \frac{\partial{J}}{\partial{z_{j}^{l}}} \cdot \frac{\partial{z_{j}^{l}}}{\partial{w_{ji}^{l}}} \\ &= \delta_{j}^{l} \cdot \frac{\partial{\left( w_{ji}^{l}a_{i}^{l-1} + b_{j}^{l} \right)}}{\partial{w_{ji}^{l}}} \\ &= \delta_{j}^{l} \cdot a_{i}^{l-1} \end{aligned}$

$\frac{\partial{J}}{\partial{w_{ji}^{l}}} = \delta_{j}^{l} \cdot a_{i}^{l-1}$

最後に、損失関数を使用してバイアスの勾配を計算します：

$\begin{aligned} \frac{\partial{J}}{\partial{b_{j}^{l}}} &= \frac{\partial{J}}{\partial{z_{j}^{l}}} \cdot \frac{\partial{z_{j}^{l}}}{\partial{b_{j}^{l}}} \\ &= \delta_{j}^{l} \cdot \frac{\partial{w_{ji}^{l} a_{i}^{l-1} + b_{j}^{l}}}{\partial{b_{j}^{l}}} \\ &=\delta_{j}^{l} \end{aligned}$