本文严重参考了 CSDN 反向传播算法(过程及公式推导)
基本定义#
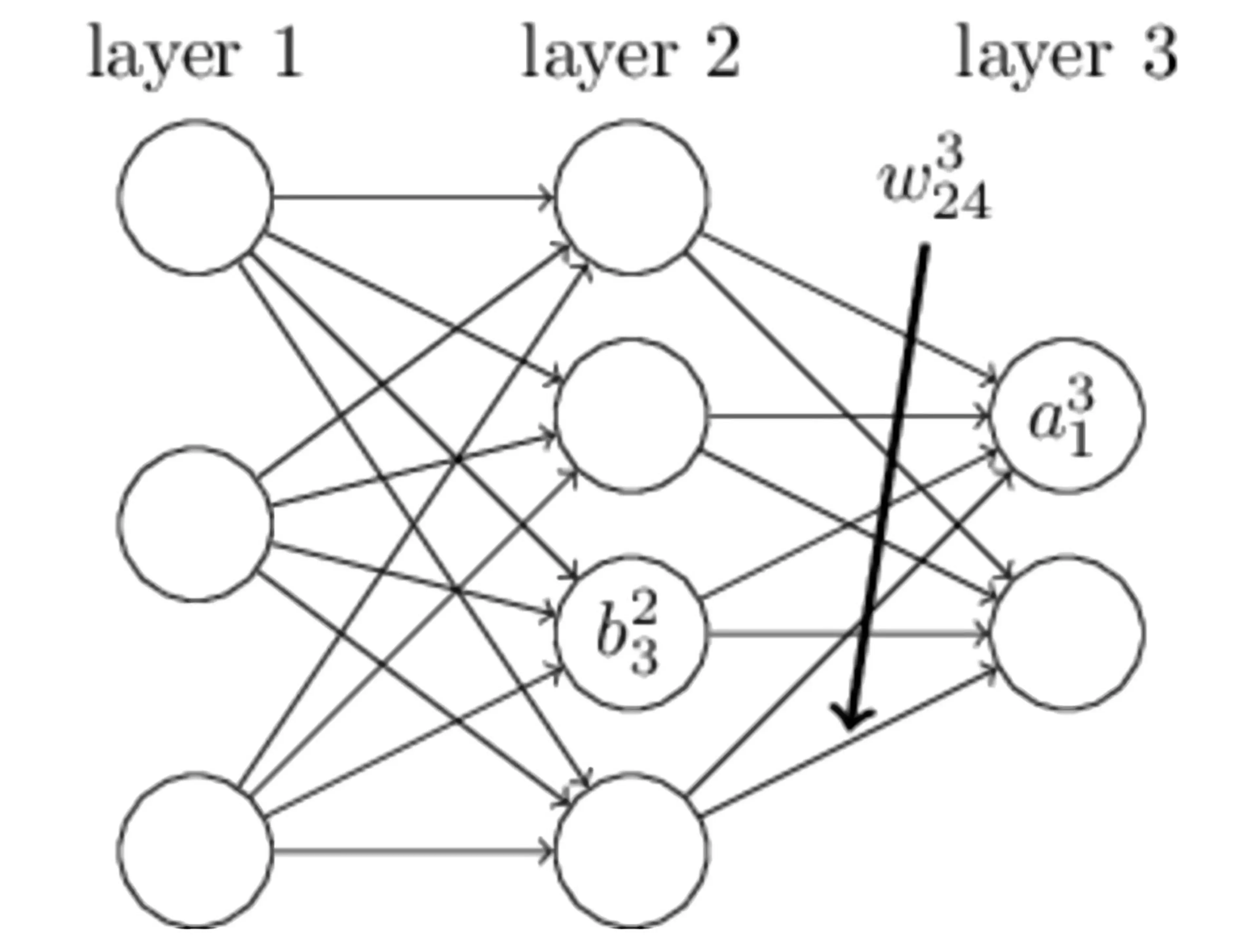
在上图所示的简单神经网络中,layer 1 是输入层,layer 2 是隐藏层,layer 3是输出层。我们用上图来阐述一些变量名称的意义:
| 名称 | 含义 |
|---|
| bil | 第 l 层的第 i 个神经元的偏置 |
| wjil | 第 l−1 层的第 i 个神经元连接第 l 层的第 j 个神经元 |
| zil | 第 l 层的第 i 个神经元的输入 |
| ail | 第 l 层的第 i 个神经元的输出 |
| σ | 激活函数 |
通过上面的定义,我们可以知道:
zjl=∑iwjilail−1+bjl
ajl=σzjl=σ(∑iwjilail−1+bjl)
我们令损失函数为二次代价函数 (Quadratic Cost Function) :
J=2n1∑x∣∣y(x)−aL(x)∣∣2
其中,x 表示输入样本,y(x) 表示实际分类,aL(x) 表示预测分类,L 表示网络的最大层数。当只有一个输入样本时,损失函数 J 标示为:
J=21∑x∣∣y(x)−aL(x)∣∣2
最后我们将第 l 层第 i 个神经元中产生的错误定义为:
δil≡∂zil∂J
公式推导#
损失函数对最后一层神经网络产生的错误为:
δiL=∂ziL∂J=∂aiL∂J⋅∂ziL∂aiL=∇J(aiL)σ′(ziL)
δL=∇J(aL)⊙σ′(zL)
损失函数对第 j 层网络产生的错误为:
δjl=∂zjl∂J=∂ajl∂J⋅∂zjl∂ajl=i∑∂zil+1∂J⋅∂ajl∂zil+1⋅∂zjl∂ajl=i∑δil+1⋅∂ajl∂wijl+1ajl+bil+1⋅σ′(zjl)=i∑δil+1⋅wijl+1⋅σ′(zjl)
δl=((wl+1)Tδl+1)⊙σ′(zl)
则通过损失函数我们可以计算权重的梯度为:
∂wjil∂J=∂zjl∂J⋅∂wjil∂zjl=δjl⋅∂wjil∂(wjilail−1+bjl)=δjl⋅ail−1
∂wjil∂J=δjl⋅ail−1
最后,通过损失函数计算偏执的梯度为:
∂bjl∂J=∂zjl∂J⋅∂bjl∂zjl=δjl⋅∂bjl∂wjilail−1+bjl=δjl